基础算法:贪心选择
算法目标:
贪心算法和动态规划一样,经常被用以解决最优解问题。但与动态规划不同的时,贪心法在策略上仅是通过当前的信息做出选择,而不是出于整体考虑,类似动态规划得到全局信息后回溯找到全局最优解,这使得贪心选择不能保证得到的解为全局最优,但通常能得到较好的近似最优解。但有些问题使用贪心算法时可以通过一系列局部最优的选择得到全局最优,我们就可以利用这种性质简化问题的动态规划算法,降低算法的复杂性。比如像人民币纸币交易时找钱这个过程,只要从最大面值的开始抽取,依次向面值小的抽取,肯定能够抽出张数最少的人民币,这得益于银行对人民币的良好设计。活动选择、背包问题、Prim、Dijkstra等都可以应用贪心算法。
适用问题:
一般来说,一个问题具有以下两个重要的性质便可以使用贪心算法。
最优子结构。当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构。这里也能看出,如果一个问题能使用贪心算法解决,那么一般也适用动态规划。
贪心选择性质。指问题的整体最优解可以通过一系列局部最优的选择,即贪心算法得到。如何证明一个问题具有贪心选择性质是贪心算法的一大难点。
举几个栗子:
1.(非0-1)背包问题
在之前我们讲到0-1背包问题,是一个自底向上的动态规划问题,实际就是将解向量形成的每个状态都用一个表记录下来,最后得到整体问题的一个最优解,与常用的回溯算法有着很深的关系。而非0-1背包问题取消了解向量每个元素固定的0和1两个状态,而用一个条件范围内的任意值代替。通俗来说,就是背包装入的货物由不可分割的整体变为可分割的”散货“。显而易见地,如果我们从"价值/重量"比最大的开始,依次向价重比较小的尽可能地装入背包,那在背包装满时就能得到问题的最优解。那么非0-1背包问题的算法结构是:
(1)计算各货物的价值/重量比,得到从大到小的次序
(2)选择还有剩余的最大价重比的货物,装入背包
(3)重复(2)步骤,直到背包装满或者货物全部被带走
物品的价值与重量如下表所示。
| 物品(i) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 重量(wi) | 4 | 5 | 10 | 11 | 13 | 14 | 17 |
| 价值(vi) | 3 | 4 | 7 | 8 | 9 | 10 | 11 |
物品根据价值/重量比排序(从大到小)得:
| 物品(i) | 2 | 1 | 4 | 6 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|
| 重量(wi) | 5 | 4 | 11 | 14 | 10 | 13 | 17 |
| 价值(vi) | 4 | 3 | 8 | 10 | 7 | 9 | 11 |
x1
3using std::cout;4using std::cin;5using std::endl;6
7void fillin(float * values,float * weights,float cap,int n){8 float * vw = new float[n]; // 单位价值9 float * gets = new float[n]{} ; // 装入数量10 11 for(int i = 0; i < n; ++i){12 vw[i] = (float)values[i] / weights[i];13 }14 // 贪心选择15 while(cap > 0){16 int max = 0;17 while(max < n && gets[max] > 0){18 ++max;19 }20 if(max >= n) break;21
22 for(int i = max; i < n; ++i){23 if(gets[i] == 0 && vw[i] > vw[max]){24 max = i;25 }26 }27 if(weights[max] < cap){28 cap -= weights[max];29 gets[max] = weights[max];30 weights[max] = 0;31 }else{32 gets[max] = cap;33 weights[max] -= cap;34 cap = 0;35 }36 }37
38 float sum_w = 0;39 float sum_v = 0;40 for(int i = 0; i < n ; ++i){41 sum_w += gets[i];42 sum_v += gets[i] * vw[i];43 }44 45 cout << "gets = [";46 for(int i = 0; i < n ; ++i){47 cout << gets[i] << " ";48 }49 cout << "]" << endl;50 cout << "Sum_weight = " << sum_w << endl;51 cout << "Sum_value = "<< sum_v << endl;52
53 delete [] gets;54 delete [] vw;55}56
57int main(){58 float values[] = {3,4,7,8,9,10,11};59 float weights[] = {4,5,10,11,13,14,17};60 float cap = 20;61 fillin(values,weights,cap,sizeof(values)/sizeof(float));62 63 return 0;64}
2.Prim算法
问题描述与分析:
经典的Prim算法基于贪心选择构造最小生成树。对于一个无向连通图,如何找到一个边的权值和最小的生成树?约束条件只有一个,即生成树要求其中无环且包含图的全部结点,目标是求取权值和最小。而Prim算法的结构是:
(1)选取一个初始结点
(2)从被选取结点连接未选取结点的边中选择
(3)重复(2)步骤,直到所有结点存在于选取顶点列表中。
从Prim算法的应用可以看到,每次边的选择其实并不会影响到后续边的选择。因为约束条件没有改变,每次从待选边中被抛弃的边不可能出现再后续待选边中,即选择是安全的。每一阶段的状态转移仅依赖于迁移状态的最佳结果而不受到该状态路径的影响,这样持续的状态转移必能够导向全局最优解。以下图为例
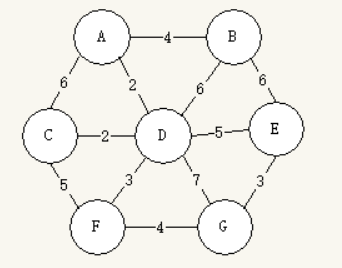
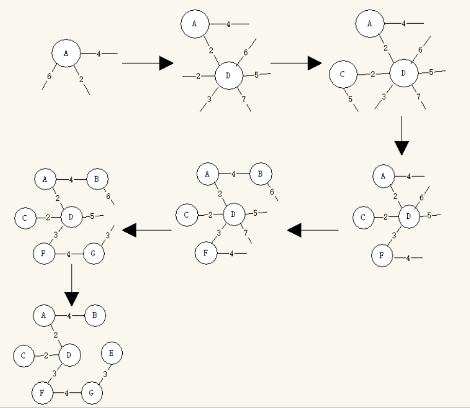
Prim算法
代码示例(C++):
xxxxxxxxxx861
4using std::cout;5using std::cin;6using std::endl;7using std::vector;8
9// 打印10void printMST(vector<std::pair<int,int>> MST , vector<char> vetexes){11 cout << "MST: ";12 for(auto i : MST){13 cout << "<" << vetexes[i.first] << "," << vetexes[i.second] << ">" ;14 }15 cout << endl;16}17
18
19// 算法执行20vector<std::pair<int,int>> execute(vector<vector<int>> diagram,vector<char> vetexes){21 vector<std::pair<int,int>> selected_edges;22
23 if(vetexes.size() == 1 || vetexes.size() == 0){24 return selected_edges; 25 }26
27 auto visited = new int[vetexes.size()]();28 visited[0] = 1;29 std::pair<int,int> min_edge ;30 while(selected_edges.size() < vetexes.size()-1){31 int min_weight = 9999;32 // 检查已添加的顶点的边33 for(int i = 0 ; i < vetexes.size() ; ++i){34 if(visited[i] == 1){35 for(int j = 0; j < vetexes.size() ; ++j){36 if(diagram[i][j] > 0 && visited[j] == 0){37 if(diagram[i][j] < min_weight ){38 min_weight = diagram[i][j];39 min_edge = {i,j};40 }41 }42 }43 }44 }45 selected_edges.push_back(min_edge);46 visited[min_edge.second] = 1;47 }48 delete [] visited;49 return selected_edges;50}51
52void Prim(vector<vector<int>> diagram,vector<char> vetexes){53 int count = vetexes.size();54 vector<std::pair<int,int>> MST;55 MST.reserve(count);56
57 MST = execute(diagram,vetexes);58 if(MST.size() < count-1){59 cout << "非连通图,无最小生成树" << endl;60 return;61 }62 63 printMST(MST,vetexes);64 int sum = 0;65 for(int i = 0 ; i < MST.size() ; ++i){66 sum+=diagram[MST[i].first][MST[i].second];67 }68 cout << "MST_weight = " << sum << endl;69
70}71
72int main(){73 // 示例74 vector<vector<int>> diagram = {75 {0,4,6,2,-1,-1,-1},76 {4,0,-1,6,6,-1,-1},77 {6,-1,0,2,-1,5,-1},78 {2,6,2,0,5,3,7},79 {-1,6,-1,5,0,-1,3},80 {-1,-1,5,3,-1,0,4},81 {-1,-1,-1,7,3,4,0}82 };83 vector<char> vetexes = {'A','B','C','D','E','F','G'}; 84 Prim(diagram,vetexes); 85 return 0;86}
本来在这里还想补充一个关于哈夫曼编码的c实现,但最近手头事情挺多,待后面再补充吧qwq
😳